反向传播

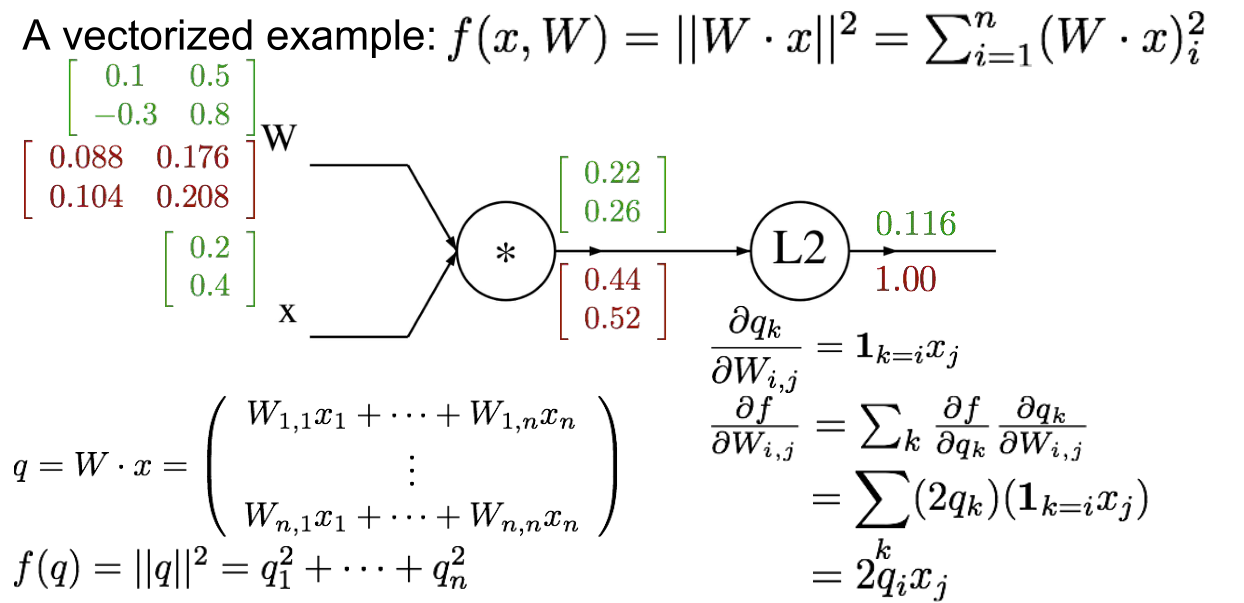
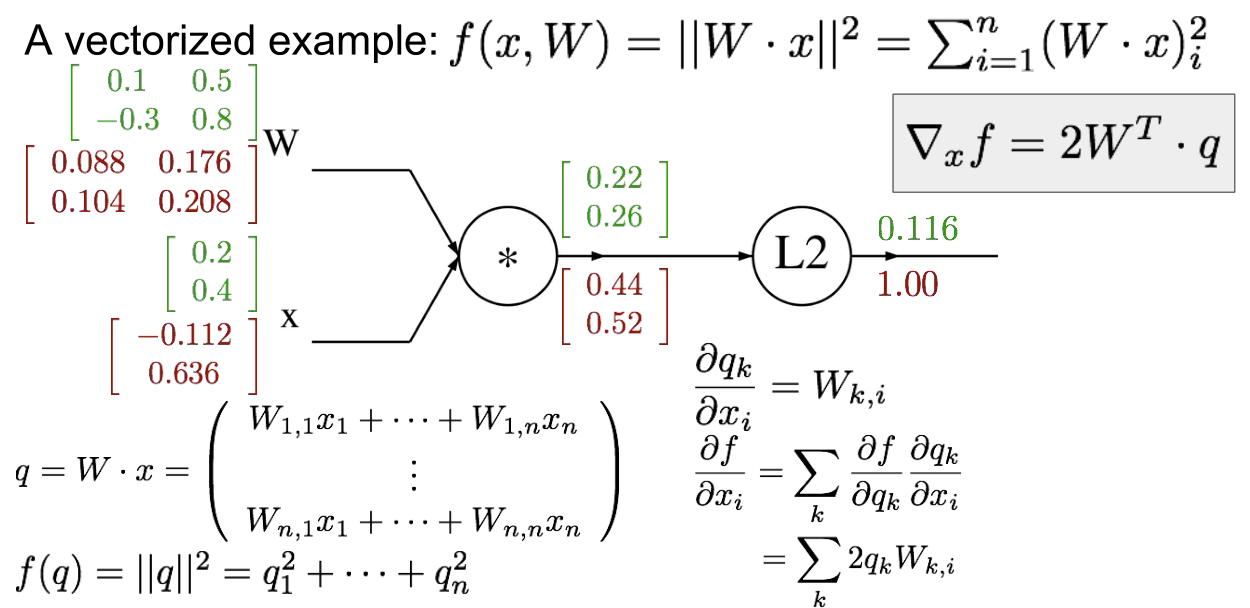
已经讲过用函数f定义一个分类器，函数f的参数是权重矩阵W，输入数据x并对你想要分类的每个类别都输出一个对应的得分向量。还可以定义一个损失函数（svm）对模型预测结果满意或是不满意的程度，然后用它定义一个总的损失函数L，L是由训练数据带来的损失结合一个正则项得到的，正则项表示模型的复杂程度，为了更好地泛化，我们倾向取简单的模型，所以现在想要找到与最小损失对应的参数W。想要最小化损失函数，为了做到这一点，我们想要找到L在W方向的梯度。即为最优化，沿着最陡的下降方向，即梯度的负方向，来一步步迭代，这样就能沿着损失函数从上往下，走到最低点。

梯度计算：有限差分估计，解析梯度计算。

如何计算复杂函数的解析梯度，用到一个叫计算图的框架。大体上，计算图就是我们用这类图来表示任意函数，其中图的节点，表示我们要执行的每一步计算。

好处：用计算图来表示一个函数，就能用反向传播技术，递归地调用链式法则来计算计算图中每个变量的梯度。

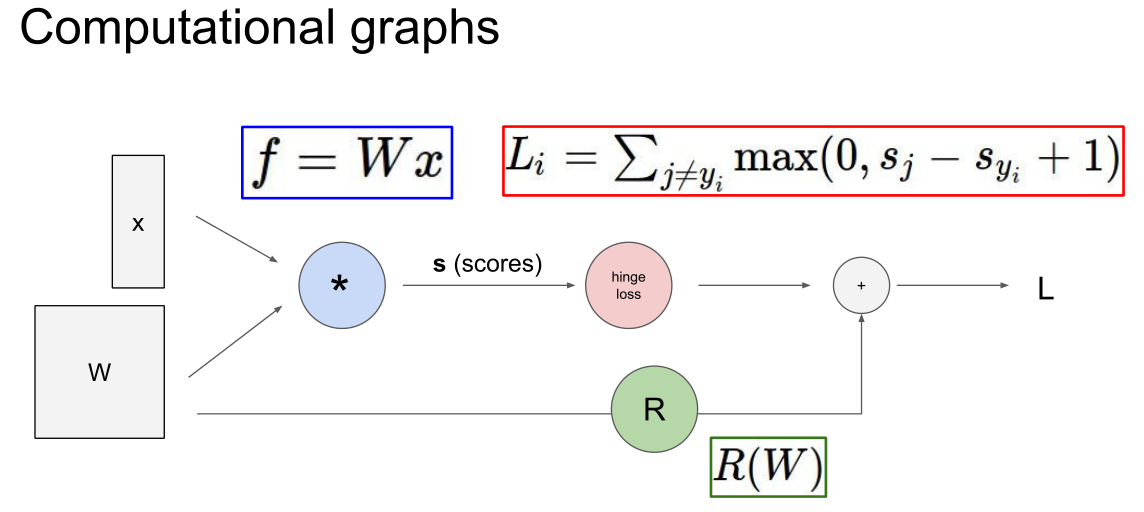
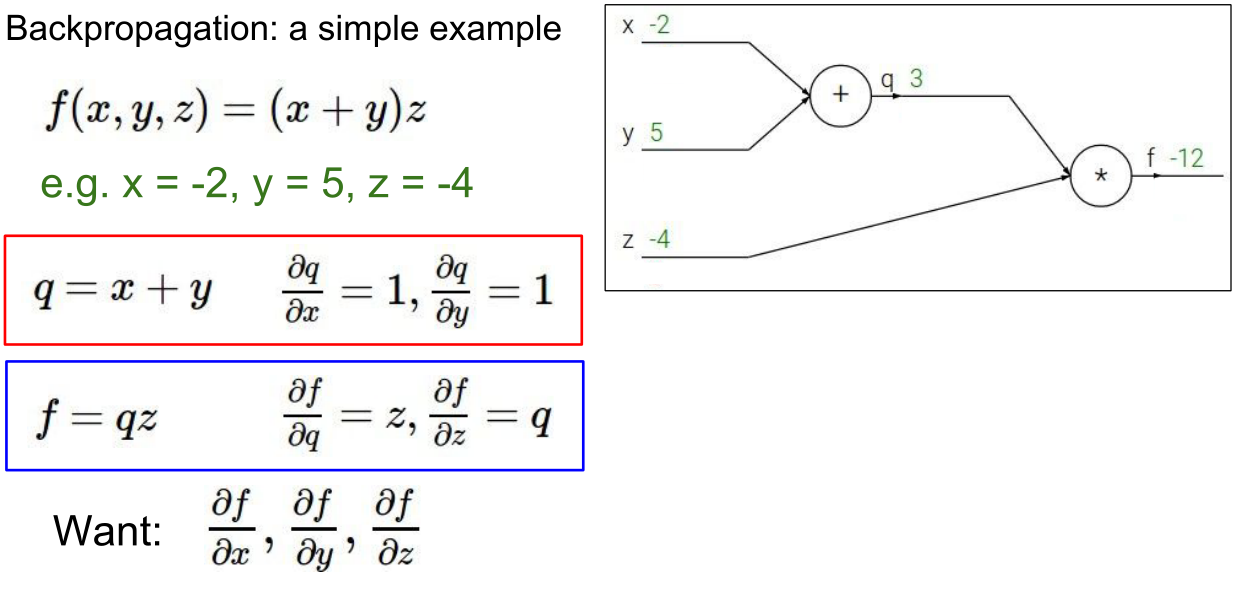
在每一个节点上计算我们所需的本地梯度，然后跟踪这个梯度，在反向传播过程中，我们接收从上游传回来的这个梯度值，我们直接用这个值乘以本地梯度，然后得到我们想要传回连接点的值，在下一个节点进行反向传播时，我们不考虑除了直接相连的节点之外的任何东西。

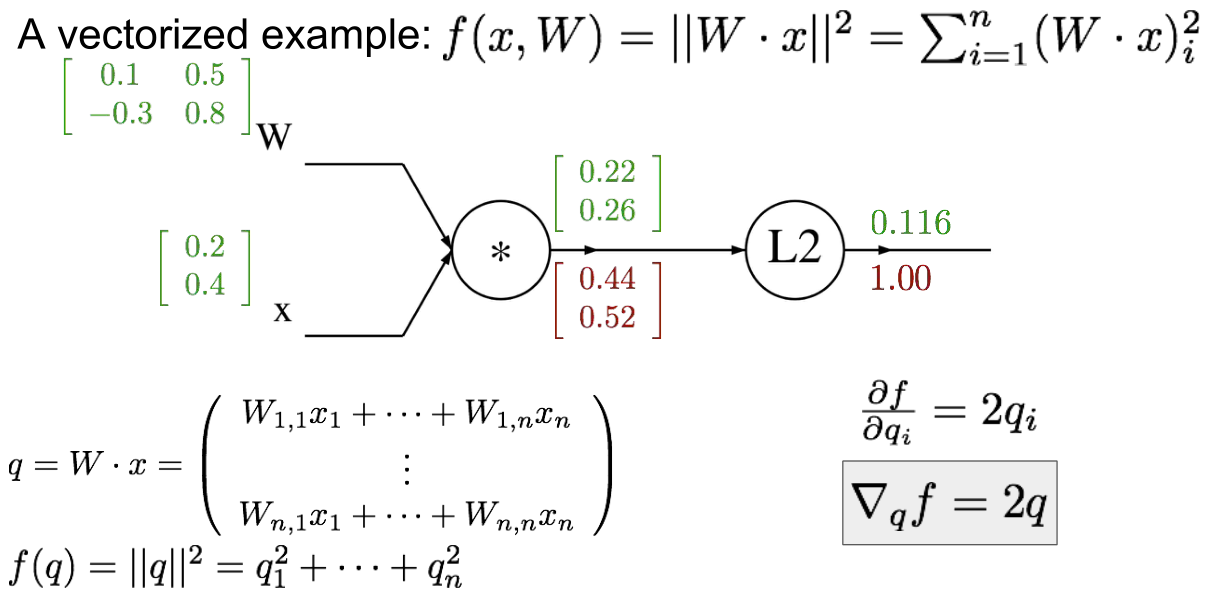
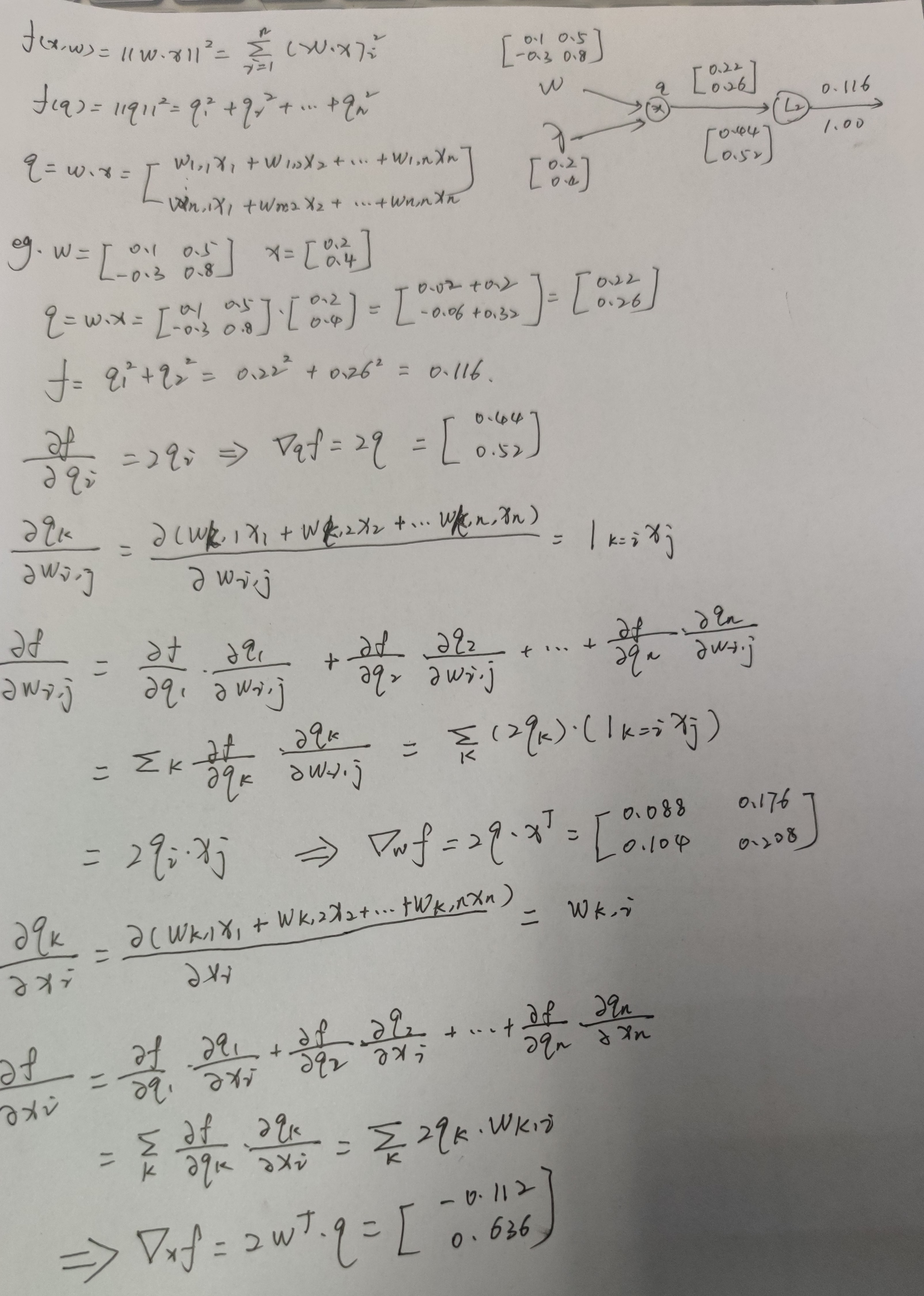
神经网络

一般来说，神经网络就是由简单函数构成的一组函数在顶层堆叠在一起，我们用一种层次化的方式将它们堆叠起来，为了形成一个更复杂的非线性函数。这就是最基本的多阶段分层计算。

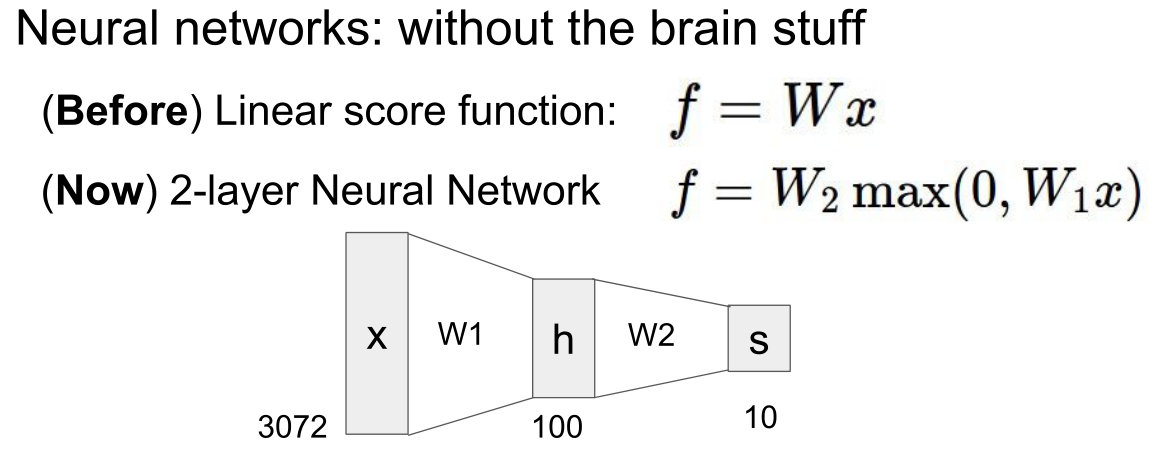
计算图里的节点相互连接，我们需要输入“信号x”，所有x的输入量比如x0、x1、x2等，采用比如赋予权重W的方法，叠加汇合到一起，将结果整合起来后得到一个激活函数，将激活函数应用在神经元的端部，得到的值作为输出。

笔记

官方笔记