训练神经网络(上)
Contents
训练神经网络(上)
激活函数
任意特定层产生的输出是输入数据在全连接层或者卷积层乘上权重值,然后将结果输入一个激活函数或者非线性单元,下面给出了一些激活函数:
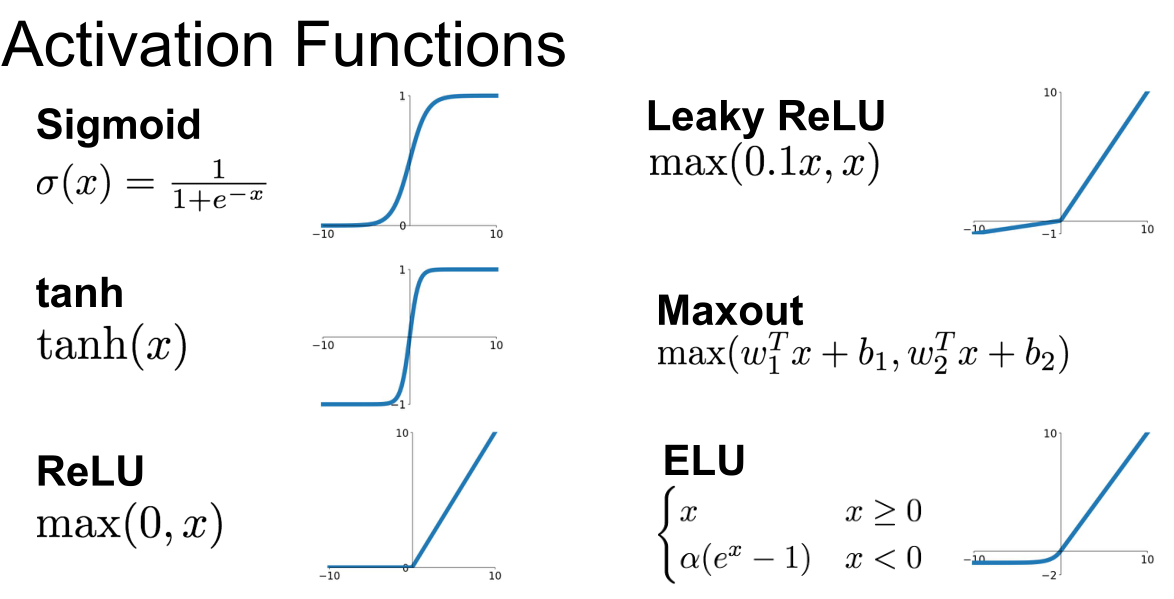

sigmod函数
每个元素输入到这个函数中,会被压缩在[0,1]范围内,如果有非常大的输入值,那么输出将会接近1;如果有绝对值很大的负的输入值,那么输出将会接近0。
存在的问题:
-
饱和神经元将使梯度消失
当X的输入是一个很大的正值和很小的负值时,它们会位于sigmoid函数的平滑区域(从图像上看),这些区域会使梯度消失,从而无法得到梯度流的反馈。
-
sigmoid函数是一个非零中心的函数
意味着所有关于X的梯度,因为它们全是正数或负数,在更新的时候只能往一个方向移动,这种情况下梯度更新的效率会非常低。假设最佳的W实际上是蓝色的向量,但是我们的梯度更新只能沿着红色的曲线走,目标也是得到最佳的W,但是这样的更新效率非常低。
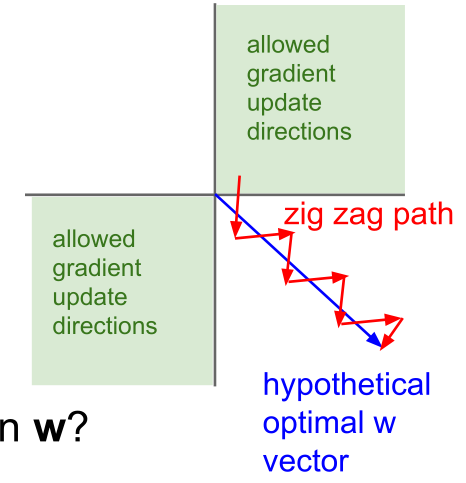

-
使用指数函数的计算代价有点高。
tanh函数
它与sigmoid函数很相似,只不过它的值被压缩在[-1,1]的范围内,所以主要的不同就是tanh函数是以0为中心,它就不会出现sigmoid函数的第二个问题,但是它仍会存在饱和使梯度消失的问题。
ReLU函数
f(x)=max(0,x)。它在输入上按元素进行操作,如果输入的是负数,将会得到结果0;如果输入的是正数,结果还是所输入的数。看到ReLU函数的图像可以知道它在正数区域不会出现产生饱和现象,这是很大的优势,而且它的计算成本也不高,并且它比sigmoid函数和tanh函数收敛快得多(大约6倍)。
存在的问题:
- 还是出现了不以0为中心的问题;
- 负半轴还是会出现饱和现象。
数据预处理
接下来讨论关于数据预处理的问题,一些数据预处理的标准类型是实现零均值化数据和用标准差归一化数据:
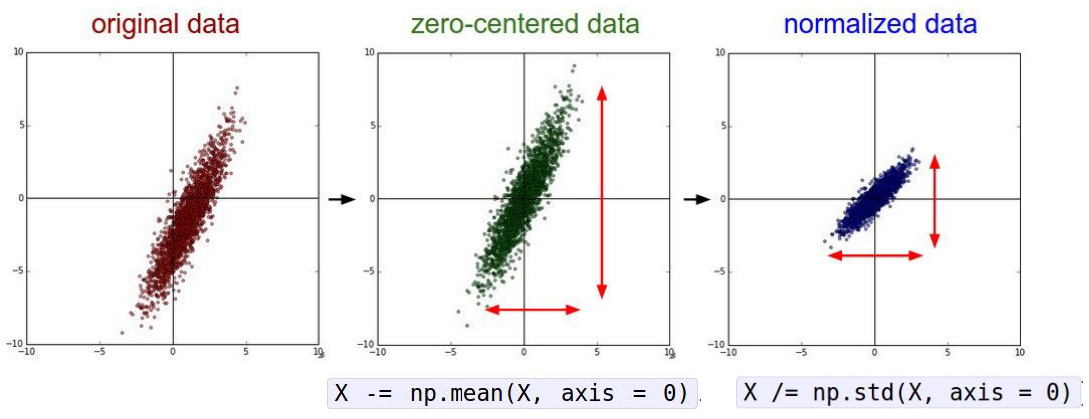

实际上,还会看到像是PCA或是数据的白化,一直以来坚持使用零均值化而不做归一化处理或是更复杂的处理;因为,一般来说,对于图像不会真的想要所有的输入,用像素值来举例,将其投影到一个更为低维的空间,这个空间有正在处理的各种新的特征,只想在空间上应用卷积网络并且得到原图像的空间结构。
在训练阶段决定均值,然后会将一样的均值应用到测试数据中去,会从训练数据中得到相同的经验均值来归一化。
总结来说,一般对于图像,做的就是零均值化的预处理,可以减去整张均值图像的值;对一些网络,也通过减去单通道的均值代替用整张均值图像来将图像集零中心化。
初始化网络权重
当使用零为权值,W的初始值会发生什么:每个神经元将在输入的数据上有相同的操作,接着将输出相同的数值并且得到相同的梯度;因为用相同的方式进行更新将得到完全相同的神经元,而我们期望的是不同的神经元学习到不同的知识。
所以,可以尝试将其改变为所有权重是一个小的随机数,从一个概率分布中抽样W=0.01*np.random.randn(D,H),这里从标准高斯分布中抽样,这样的参数适合在小型网络中使用;下面给出一个例子:
初始化一个10层神经网络,每层有500个神经元,使用tanh非线性激活函数,用小的随机数来初始化,实现过程如下:
|
|
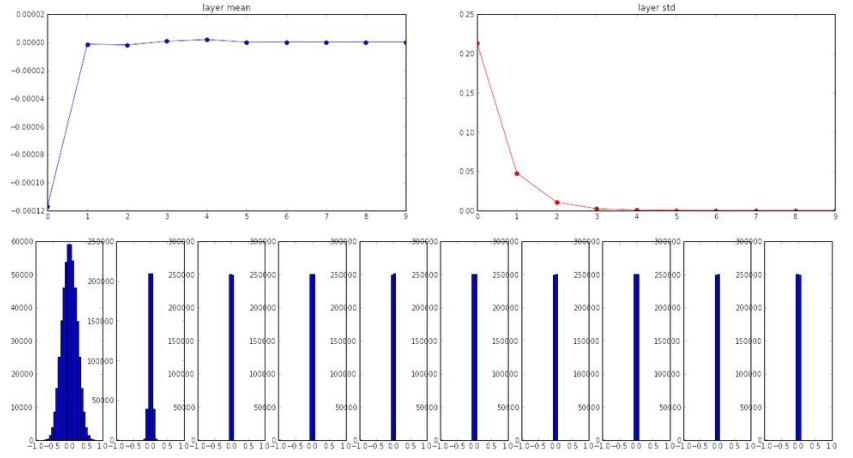

可以看到这里的输出,均值总是在0附近,所以因为tanh函数是以0为中心,这就变得很有意义;而标准差会不断缩小,快速逼近0;从上图中显示的每层均值和标准差,展示了每一层激活值的概率分布。
可以看到第一层有一个合理的高斯分布,而当每一层乘以一个W(一些小随机数)后,随着一次次乘法,迅速的缩小到最后是一堆0,所有的激活值都变成0,这并不是所期望的。
反向传播的梯度是上层的梯度乘以本层的梯度(W乘以X),反向传播的所有层基本上是在做上层梯度和权重的乘法来得到下层的梯度;由于这个原因,不断乘以W基本是相同的现象,所有数据越来越小,梯度和上层梯度趋向于0。
如果尝试用增大权重来解决这个问题,不在用0.01,而是用1来替代W = np.random.randn(fan_in, fan_out) * 1.0 ,会出现下面的情况:
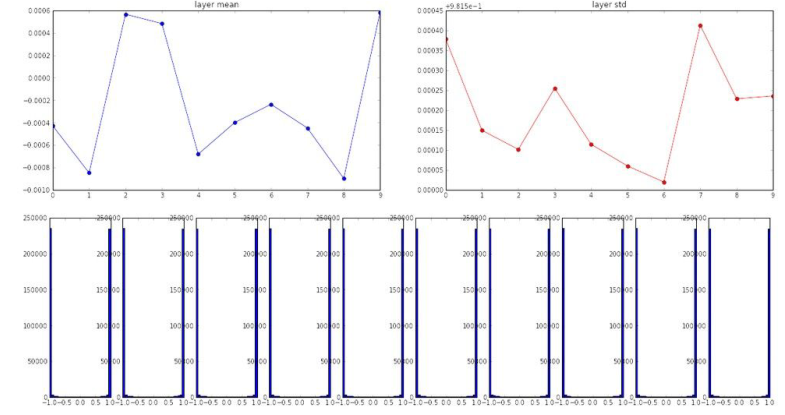

由于权重增大,就会始终处于饱和状态,不管是tanh的负方向还是正方向;如果观察激活值在每一层的分布,它们会趋向于-1或1。
初始化权重一个很好的经验是Xavier initialization。
W=np.random.randn(fan_in, fan_out)/np.sqrt(fan_in),这种方法在每一层都能大概获得一个高斯分布。
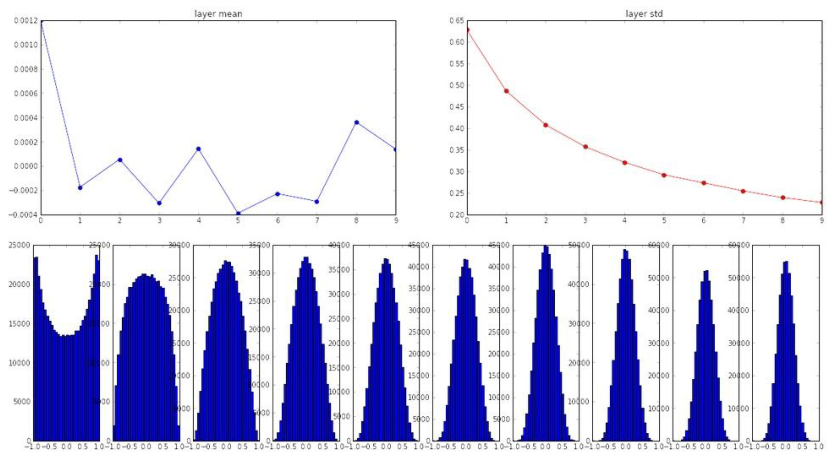

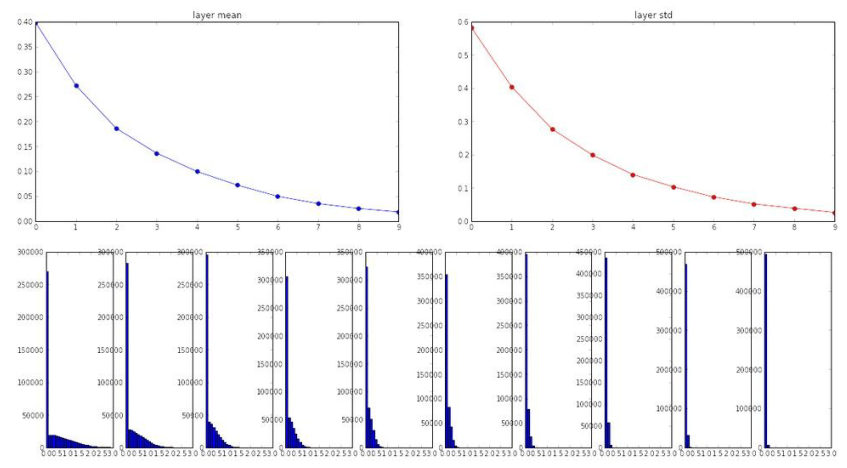
上述是使用tanh激活函数时的情况,当使用ReLU激活函数时,它会“消除”一半的神经元,所以实际是把得到的方差减半,将再次看到分布趋向于0。

批量归一化
观察学习过程
我们已经定义了网络结构,现在将要讨论如何监视训练并在训练过程中调整这些超参数以获得最好的学习结果。
一直以来第一件事是进行数据的预处理,然后要做的是初始化网络,网络进行前向传播并确实最终损失函数是合理的,接下来做的是加入0正则化项,然后开始训练,需要确定最优的学习率(一般设置在1e-3到1e-5之间)。
那么到底如何选择这些超参数呢?
策略是对任何超参数执行交叉验证,交叉验证是在训练集上训练然后在验证集验证,观察这些超参数的实验结果。
首先,选择相当分散的数值,然后用几个epoch的迭代去学习,通过几个epoch可以知道哪些超参数有效,就可以做出相应的调整;
接着,花长时间来运行并在区间进行进一步精确搜索;
在训练循环中,找到一个像nan这样激增的技巧(nan表示设置的学习率过大),开始训练一些参数,在每一个迭代或epoch观察代价,如果出现一个远大于初始代价的值,就可以知道这不是一个正确的方向,它会迅速变得非常大跳出循环停止这个参数的巡练。
另一个就是使用网格寻找,对不同超参数的采样,可以对每个超参数的一组固定值采样,但是实际上不如使用一种随机排列的方式,对每一个超参数在一定范围内进行随机值采样, 随机更加真实,通常会对我们真正有的维度进行稍微有效的降维,接着就可以得到已有的重要变量的样本,可以看到右图中上方画出的绿色的圈比左边的网格分布要更多(绿色的圈表示较好值的位置)。
在观察每一条损失曲线的时候,学习率是重要的一个因素,可以很好的感受到哪些学习率是好的,哪些学习率是不好的,如下图所示:
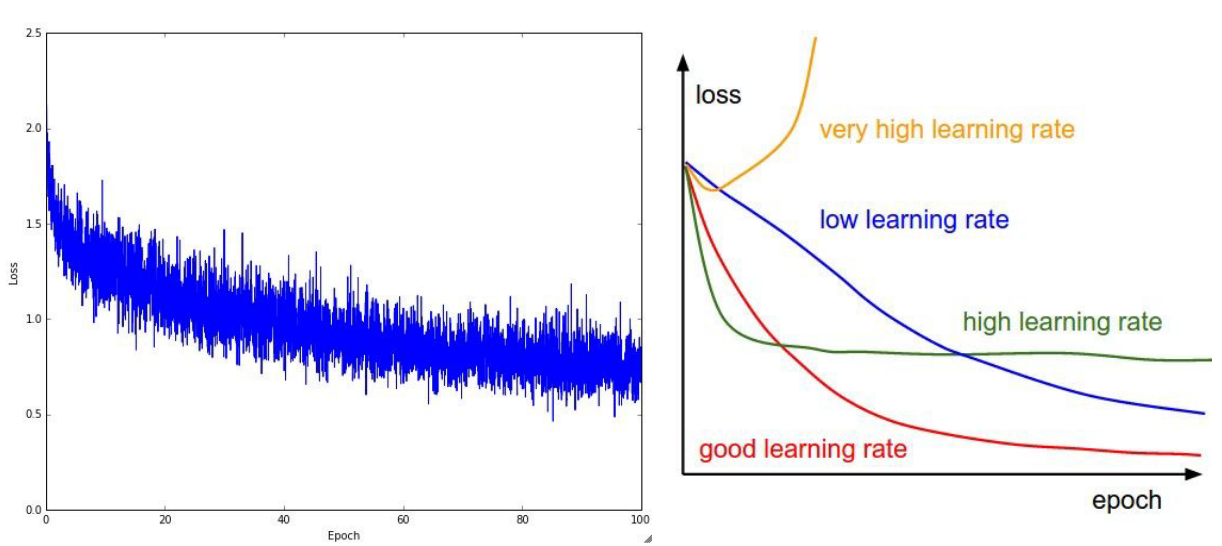

另外要提到的是,当观察每一条损失曲线的时候,如果它在一定时间内很平滑,然后突然开始训练,这可能是初始值没有设好,如下图所示:
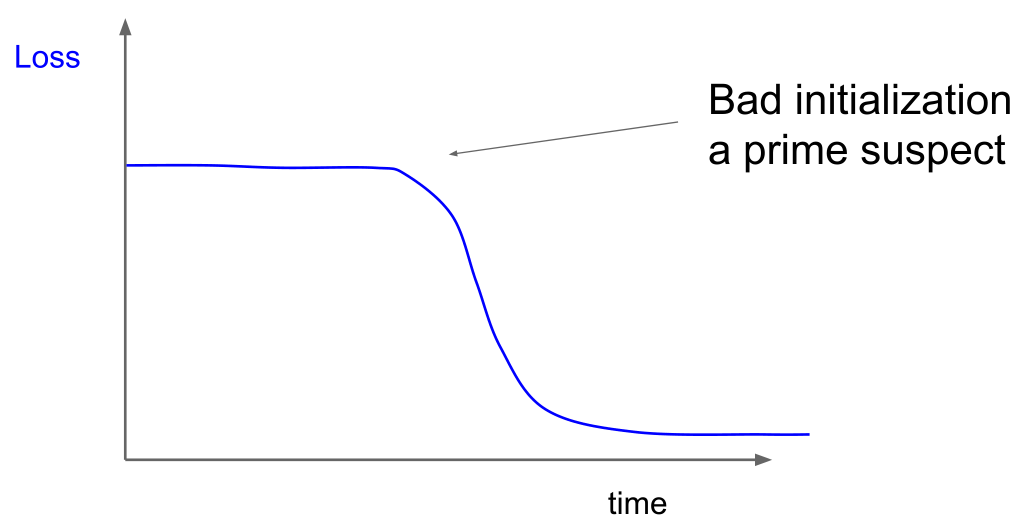

对于下面这张图,不断的积累经验就能很快的发现哪里有问题:
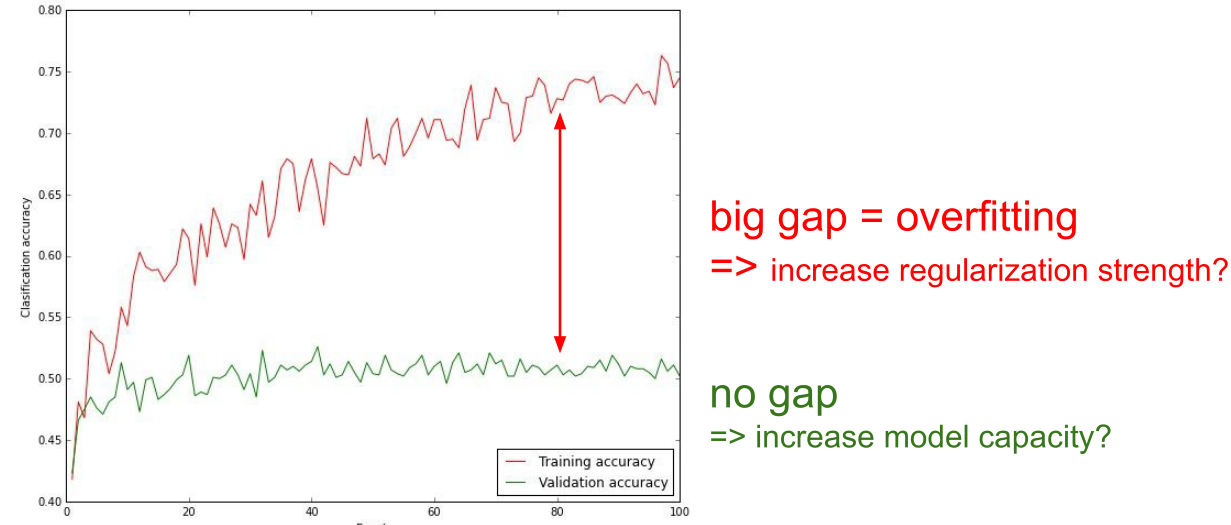

如果训练精度和验证精度间有一个很大的差值,意味着可能产生过拟合,可以试着增加正则项权重;如果没有差值,意味着没有过拟合,可以增加模型容量,这样也会提高精度。
Author kong
LastMod 2022-03-27