重新排序得到 2 的幂

给定正整数 N ，我们按任何顺序（包括原始顺序）将数字重新排序，注意其前导数字不能为零。

如果我们可以通过上述方式得到 2 的幂，返回 true；否则，返回 false。

示例 1：
1
2
输入：1
输出：true
示例 2：
1
2
输入：10
输出：false

方法一：搜索回溯 + 位运算

将 n 的十进制表示视作一个字符数组，我们可以枚举该数组的所有排列，对每个不含前导零的排列判断其对应的整数是否为 2 的幂。

这可以拆分成两个子问题：

枚举可能包含重复字符的数组的全排列
判断一个整数是否为 2 的幂

对于本题的具体实现，我们可以在递归搜索全排列的同时，计算出当前排列的已枚举的部分所对应的整数 num。在我们枚举当前排列的下一个字符 ch 时，将 ch 加到 num 的末尾，即 num = num * 10 + ch - ‘0’，然后递归进入下一层。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


def isPowerOfTwo(n: int) -> bool:
    return (n & (n - 1)) == 0

class Solution:
    def reorderedPowerOf2(self, n: int) -> bool:
        nums = sorted(list(str(n)))
        m = len(nums)
        vis = [False] * m

        def backtrack(idx: int, num: int) -> bool:
            if idx == m:
                return isPowerOfTwo(num)
            for i, ch in enumerate(nums):
                # 不能有前导零
                if (num == 0 and ch == '0') or vis[i] or (i > 0 and not vis[i - 1] and ch == nums[i - 1]):
                    continue
                vis[i] = True
                if backtrack(idx + 1, num * 10 + ord(ch) - ord('0')):
                    return True
                vis[i] = False
            return False

        return backtrack(0, 0)

复杂度分析：

时间复杂度：O(m!)。其中m=⌊log_10 n⌋+1,即n的十进制表示的长度。
空间复杂度：O(m)。我们需要 O(m) 的标记数组，同时在递归的时候栈深度会达到 O(m)，因此总空间复杂度为 O(m+m)=O(2m)=O(m)。

方法二：预处理+哈希表

由于我们可以按任何顺序将数字重新排列，因此对于两个不同的整数a和b，如果对于两个不同的整数a和b，如果其十进制表示的字符数组，从小到大排序后的结果是相同的，那么若a能够重排得到2的幂，b也可以；若a不能重排得到2的幂，那么b也不能。

进一步地，只要a和b的十进制表示的字符数组中，从0到9每个字符出现次数，在a和b中都是一样的，那么a和b能否得到2的幂的结果是一样的。

由于2^29<10^9<2^30，因此在[1,10^9] 范围内有 2^0,2^1,…,2^29一共 30 个 2 的幂。对这 30 个数的每个数，我们可以预处理其十进制表示的字符数组中从 0 到 9 每个字符的出现次数，记在一个长度为 10 的数组中，并用一哈希表记录这些数组。对于数字 n，我们同样统计其十进制表示的字符数组中从 0 到 9 每个字符的出现次数，然后去哈希表中查找，若存在则说明 n 可以通过重排得到 2 的幂，否则不能。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def countDigits(n: int) -> Tuple[int]:#统计对应十进制各个数字出现的次数。
    cnt = [0] * 10
    while n:
        cnt[n % 10] += 1
        n //= 10
    #tuple():列表转元组
    return tuple(cnt)
#1<<i,左移，相当于1*2^i
powerOf2Digits = {countDigits(1 << i) for i in range(30)}#集合

class Solution:
    def reorderedPowerOf2(self, n: int) -> bool:
        return countDigits(n) in powerOf2Digits

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


(0, 1, 0, 0, 0, 0, 0, 0, 0, 0)
(0, 0, 1, 0, 0, 0, 0, 0, 0, 0)
(0, 0, 0, 0, 1, 0, 0, 0, 0, 0)
(0, 0, 0, 0, 0, 0, 0, 0, 1, 0)
(0, 1, 0, 0, 0, 0, 1, 0, 0, 0)
(0, 0, 1, 1, 0, 0, 0, 0, 0, 0)
(0, 0, 0, 0, 1, 0, 1, 0, 0, 0)
(0, 1, 1, 0, 0, 0, 0, 0, 1, 0)
(0, 0, 1, 0, 0, 1, 1, 0, 0, 0)
(0, 1, 1, 0, 0, 1, 0, 0, 0, 0)
(1, 1, 1, 0, 1, 0, 0, 0, 0, 0)
(1, 0, 1, 0, 1, 0, 0, 0, 1, 0)
(1, 0, 0, 0, 1, 0, 1, 0, 0, 1)
(0, 1, 1, 0, 0, 0, 0, 0, 1, 1)
(0, 1, 0, 1, 1, 0, 1, 0, 1, 0)
(0, 0, 1, 1, 0, 0, 1, 1, 1, 0)
(0, 0, 0, 1, 0, 2, 2, 0, 0, 0)
(1, 2, 1, 1, 0, 0, 0, 1, 0, 0)
(0, 1, 2, 0, 2, 0, 1, 0, 0, 0)
(0, 0, 2, 0, 1, 1, 0, 0, 2, 0)
(1, 1, 0, 0, 1, 1, 1, 1, 1, 0)
(1, 1, 2, 0, 0, 1, 0, 1, 0, 1)
(1, 1, 0, 1, 3, 0, 0, 0, 0, 1)
(1, 0, 0, 1, 0, 0, 1, 0, 4, 0)
(0, 2, 1, 0, 0, 0, 2, 3, 0, 0)
(0, 0, 1, 3, 2, 2, 0, 0, 0, 0)
(1, 1, 0, 0, 1, 0, 2, 1, 2, 0)
(0, 2, 2, 1, 1, 0, 0, 2, 1, 0)
(0, 0, 1, 1, 2, 2, 2, 0, 1, 0)
(1, 1, 1, 1, 0, 1, 1, 1, 1, 1)
{(0, 1, 0, 0, 0, 0, 0, 0, 0, 0), (0, 1, 1, 0, 0, 0, 0, 0, 1, 0), (0, 1, 2, 0, 2, 0, 1, 0, 0, 0), (1, 1, 0, 0, 1, 0, 2, 1, 2, 0), (0, 0, 0, 1, 0, 2, 2, 0, 0, 0), (1, 2, 1, 1, 0, 0, 0, 1, 0, 0), (0, 0, 1, 0, 0, 0, 0, 0, 0, 0), (0, 2, 2, 1, 1, 0, 0, 2, 1, 0), (0, 1, 0, 1, 1, 0, 1, 0, 1, 0), (0, 0, 0, 0, 0, 0, 0, 0, 1, 0), (0, 0, 0, 0, 1, 0, 0, 0, 0, 0), (0, 2, 1, 0, 0, 0, 2, 3, 0, 0), (0, 1, 0, 0, 0, 0, 1, 0, 0, 0), (0, 1, 1, 0, 0, 1, 0, 0, 0, 0), (0, 0, 1, 1, 0, 0, 1, 1, 1, 0), (1, 1, 0, 0, 1, 1, 1, 1, 1, 0), (0, 0, 1, 3, 2, 2, 0, 0, 0, 0), (0, 0, 1, 1, 0, 0, 0, 0, 0, 0), (1, 1, 1, 1, 0, 1, 1, 1, 1, 1), (0, 0, 1, 1, 2, 2, 2, 0, 1, 0), (0, 0, 0, 0, 1, 0, 1, 0, 0, 0), (0, 1, 1, 0, 0, 0, 0, 0, 1, 1), (0, 0, 1, 0, 0, 1, 1, 0, 0, 0), (1, 1, 0, 1, 3, 0, 0, 0, 0, 1), (1, 0, 0, 1, 0, 0, 1, 0, 4, 0), (0, 0, 2, 0, 1, 1, 0, 0, 2, 0), (1, 0, 1, 0, 1, 0, 0, 0, 1, 0), (1, 1, 2, 0, 0, 1, 0, 1, 0, 1), (1, 1, 1, 0, 1, 0, 0, 0, 0, 0), (1, 0, 0, 0, 1, 0, 1, 0, 0, 1)}
(0, 0, 0, 0, 1, 0, 1, 0, 0, 0)
True

复杂度分析

时间复杂度O(logn)。统计 n 的每个数字的出现次数需要 O(logn) 的时间。
空间复杂度：O(1)。

向左位移

‘«’ 操作符将执行按位的“左移”，即左操作数的值被右操作数给出的位数移动到左：
1
2
3
4
5
6
7
 #2 = 0b10
 2 << 2
 #输出: 8
 #8 = 0b1000

 bin(2 << 2)
 #输出: 0b1000
执行1的左位移位相当于乘以2
1
2
 7 << 1
 #输出: 14
执行n的左位移位相当于乘以2**n ：
1
2
 3 << 4
 #输出: 48

2的幂

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n = 2x ，则认为 n 是 2 的幂次方。

提示：

-2^31 <= n <= 2^31 - 1

示例 1：
1
2
3
输入：n = 1
输出：true
解释：20 = 1
示例 2：
1
2
3
输入：n = 16
输出：true
解释：24 = 16

方法一：二进制表示

思路与算法：

一个数n是2的幂，当且仅当n是正整数，并且n的二进制表示中包含1个1。

因此可以考虑为运算，将n的二进制表示中最低位的那个1提取出来，再判断剩余的数值是否是0即可。

下面介绍两种常见的与二进制表示中最低位相关的位运算技巧：

n & (n-1):其中&表示按位与运算（两个1为1，其余为0）。该运算技巧可以直接将n的二进制表示的最低位1移除，它的原理如下：

假设n的二进制表示为：(a10…0)₂,其中a表示若干个高位，1表示最低位的那个1,那么n-1的二进制为(a01…1)₂,将(a10…0)₂和(a01…1)₂进行按位与运算，高位a不变，在这之后的所有位都会变为0，这样就将最低位的那个1移除了。

因此，如果n是正整数并且n & (n-1) = 0，那么n就是2的幂。
1 2 3

class Solution: def isPowerOfTwo(self, n: int) -> bool: return n > 0 and (n & (n - 1)) == 0
n & (-n):其中-n是n的相反数，是一个负数。该位运算技巧可以直接获取n二进制的最低位的1，它的原理为：

假设n的二进制为：(a10…0)₂，那么-n的二进制为(a'01…1)₂+(1)₂=(a'10…0)₂,其中a‘为a的每一位取反，将(a10…0)₂和(a'10…0)₂进行按位与运算，高位全部变为0，最低位的1以及之后的所有0不变，最低位的1以及之后的所有0不变，这样就获取了n二进制表示的最低位的1。

因此，如果n是正整数并且n & (-n) = n，那么n就是2的幂。
1 2 3

class Solution: def isPowerOfTwo(self, n: int) -> bool: return n > 0 and (n & -n) == n

复杂度分析：

时间复杂度：O(1)
空间复杂度：O(1)

方法二：判断是否为最大2的幂的约数

思路和算法：

除了使用二进制表示判断之外，还有一种较为取巧的方法。

在题目给定的32位有符的整数的范围内，最大的2的幂为2^30=1073741824。我们只需判断n是否是2^30的约数即可。

1
2
3
4
5
6


class Solution:

    BIG = 2**30

    def isPowerOfTwo(self, n: int) -> bool:
        return n > 0 and Solution.BIG % n == 0

复杂度分析：

时间复杂度：O(1)
空间复杂度：O(1)

全排列

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例 2：

输入：nums = [0,1] 输出：[[0,1],[1,0]] 示例 3：

输入：nums = [1] 输出：[[1]]

提示：

1 <= nums.length <= 6 -10 <= nums[i] <= 10 nums 中的所有整数互不相同

预备知识：

`回溯法`

一种通过探索所有可能候选解来找出所有的解的算法。如果候选解被确认不是一个解（或者至少不是最后一个解），回溯算法会通过

思路和算法：

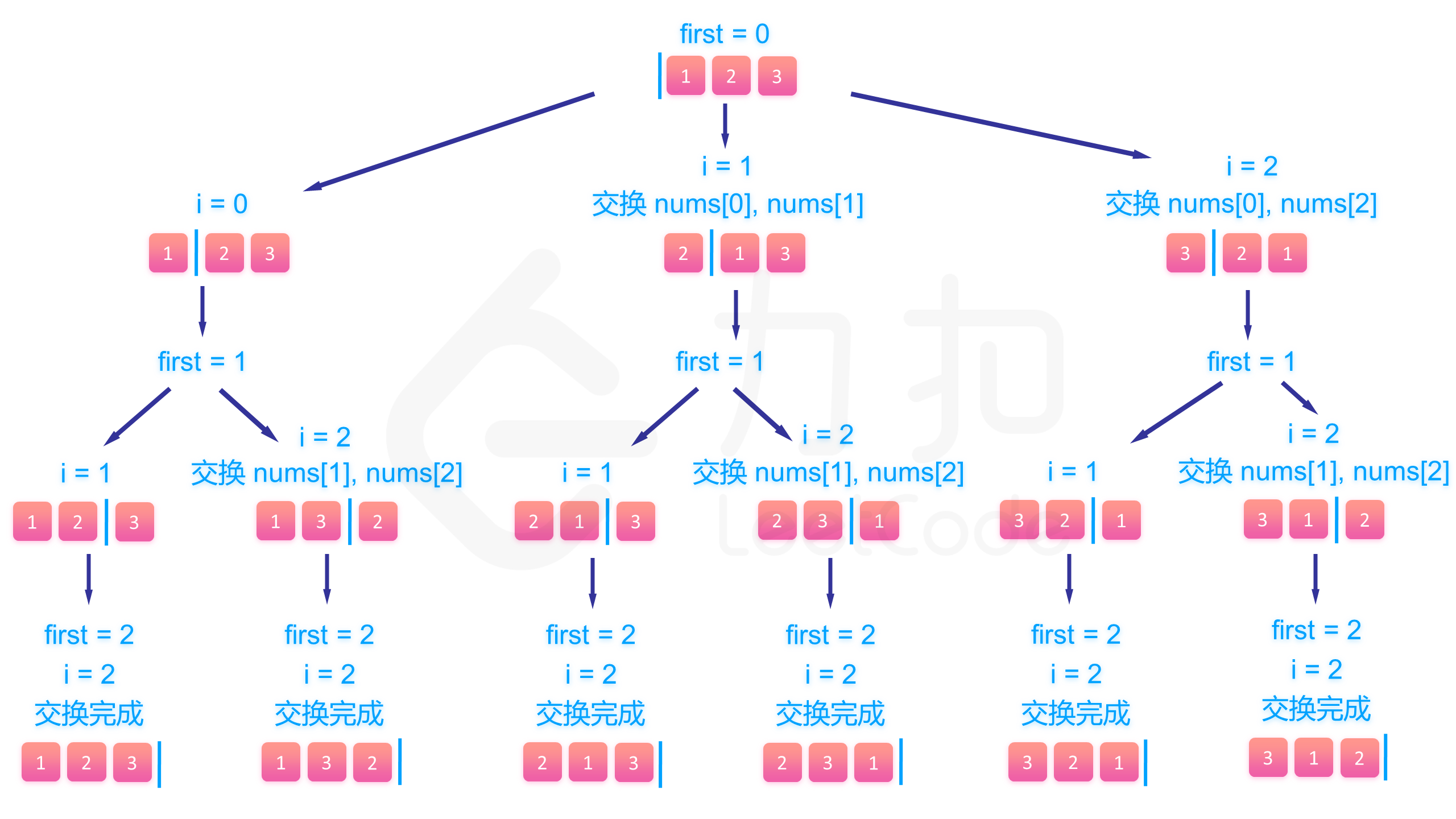
问题可以看做n个排列成一行的空格，需要从左往右依次填入题目给定的n个数，每个数只能使用一次。可以很直接的想到一种穷举算法，即从左到右每一个位置都依次尝试填入一个数，看能不能填完这n个空格，在程序中使用回溯法来模拟这个过程。

定义递归函数backtrack(first,output)表示从左向右填到first个位置，当前排列为output。那么整个递归函数分为两个情况：

如果first=n，说明已经填完n个位置（注意下标从0开始），找到了一个可行的解，将output放入答案数组中，递归结束。
如果first<n，应考虑这第first个位置要填那个数。根据题目要求我们不能填已经填过的数，因为可以想到：定义一个标记数组vis[]来标记已经填过的数，那么在填第first个数的时候，遍历题目给定的n个数，如果这个数美原油被标记过，就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数backtrack(first+1,output)。回溯的时候要撤销这一个位置填的数以及标记，并继续尝试其他未被标记过的数

使用标记数组来处理填过的数是一个很直观的思路，但是标记数组增加了算法的空间复杂度。我们可以将题目给定的n个数的数组nums划分为左右两个部分，左边的表示已经填过的数，右边表示待填的数，在回溯的时候只要动态的维护这个数组即可。

具体来说，假设我们已经填到第first个位置，那么nums数组中[0,first-1]是已填过的数的集合，[first,n-1]是待填的数的集合。尝试用[first,n-1]的数去填第first个数，假设待填的数的下标为i，那么填完以后，我们将第i个数和第first个数交换，即使能够在填第first+1个数和第first个数交换，即能使得在填第first+1个数的时候nums数组的[0,first]部分为已填过的数，[first+1,n-1]为待填的数，回溯的时候交换回来即能完成撤销操作。回退就是指撤销对当前数字的选择，回退到上一步，未选择的状态

举例：假设[2,5,8,9,10]这5个数要填入，已经填到第3个位置，已经填了[8,9]这两个数，那么这个数组目前为[8,9|2,5,10]这样的状态，分隔符区分了左右两个部分。假设这个位置填10，为了维护数组，我们将2和10交换，即能使得数组继续保持分隔符左边的数已经填过，右边的待填[8,9,10|2,5]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution:
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        def backtrack(first = 0):
            # 所有数都填完了
            if first == n:  
                res.append(nums[:])
            for i in range(first, n):
                # 动态维护数组
                nums[first], nums[i] = nums[i], nums[first]
                # 继续递归填下一个数
                backtrack(first + 1)
                # 撤销操作
                nums[first], nums[i] = nums[i], nums[first]
        
        n = len(nums)
        res = []
        backtrack()
        return res

复杂度分析：

时间复杂度：O(n*n!)，其中n为序列的长度
空间复杂度：O(n)。除了答案数组外，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以需要额外的空间且该空间取决于递归的深度，可知递归调用深度为O(n)。

全排列2

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2] 输出： [[1,1,2], [1,2,1], [2,1,1]] 示例 2：

输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8 -10 <= nums[i] <= 10

搜索回溯

我们将这个问题看作有 n 个排列成一行的空格，我们需要从左往右依次填入题目给定的 nn 个数，每个数只能使用一次。那么很直接的可以想到一种穷举的算法，即从左往右每一个位置都依此尝试填入一个数，看能不能填完这 n 个空格，在程序中我们可以用「回溯法」来模拟这个过程。

我们定义递归函数 backtrack(idx, perm) 表示当前排列为 perm，下一个待填入的位置是第 idx 个位置（下标从 0 开始）。那么整个递归函数分为两个情况：

如果 idx==n，说明我们已经填完了 n 个位置，找到了一个可行的解，我们将 perm 放入答案数组中，递归结束。
如果 idx<n，我们要考虑第 idx 个位置填哪个数。根据题目要求我们肯定不能填已经填过的数，因此很容易想到的一个处理手段是我们定义一个标记数组 vis 来标记已经填过的数，那么在填第 idx 个数的时候我们遍历题目给定的 n 个数，如果这个数没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 backtrack(idx + 1, perm)。搜索回溯的时候要撤销该个位置填的数以及标记，并继续尝试其他没被标记过的数。

但题目解到这里并没有满足「全排列不重复」的要求，在上述的递归函数中我们会生成大量重复的排列，因为对于第 idx 的位置，如果存在重复的数字 i，我们每次会将重复的数字都重新填上去并继续尝试导致最后答案的重复，因此我们需要处理这个情况。

要解决重复问题，只要设定一个规则，保证在填第idx个数的时候重复数字只会被填入一次即可。而在本题解中，选择对原数组排序，保证相同的数字都相邻，然后每次填入的数一定是这个数所在重复数集合中从左往右第一个未被填过的数字，即如下的判断条件：

1
2


if visited[i] or i>0 and nums[i]==nums[i-1] and not visited[i-1]:
	continue

这个判断条件保证了对于重复数的集合，一定是从左向右逐个填入的。

假设有三个重复数排完序后相邻，我们一定保证每次都是拿从左往右的第一个未被填过的数字，即整个数组的状态其实是保证了，（未填，未填，未填）到（填入，未填，未填）再到（填入，填入，未填）最后到（填入，填入，填入）的过程，因此可以达到去重的目标。

！！！

for循环保证了从数组中从前往后一个一个取值，再用if判断条件。所以nums[i - 1]一定比nums[i]先被取值和判断。如果nums[i - 1]被取值了，那vis[i - 1]会被置1，只有当递归再回退到这一层时再将它置0。每递归一层都是在寻找数组对应于递归深度位置的值，每一层里用for循环来寻找。所以当vis[i - 1] == 1时，说明nums[i - 1]和nums[i]分别属于两层递归中，也就是我们要用这两个数分别放在数组的两个位置，这时不需要去重。但是当vis[i - 1] == 0时，说明nums[i - 1]和nums[i]属于同一层递归中（只是for循环进入下一层循环），也就是我们要用这两个数放在数组中的同一个位置上，这就是我们要去重的情况。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution:
    def permuteUnique(self, nums):
        nums.sort()
        res=[]
        ans=[]
        n=len(nums)
        visited=[0]*n
        def dfs():
            if len(ans)==n:
                #不是append(ans)，区别是深拷贝和浅拷贝
                res.append(ans[::])
            for i in range(n):
                if visited[i] or i>0 and nums[i]==nums[i-1] and not visited[i-1]:
                    continue
                ans.append(nums[i])
                visited[i]=1
                dfs()
                ans.pop()
                visited[i]=0
        dfs()
        return res

复杂度分析：

时间复杂度：O(n*n!)
空间复杂度：O(n)，需要O(n)的标记数组，同时递归的时候栈深度会达到O(n)，因此总空间复杂度为O(n+n)=O(2n)=O(n)

Python位操作符

Contents

方法一：搜索回溯 + 位运算

方法二：预处理+哈希表

向左位移

2的幂

方法一：二进制表示

方法二：判断是否为最大2的幂的约数

全排列

回溯法

全排列2

搜索回溯

`回溯法`