MATLAB
Contents
MATLAB变量命名规则

MATLAB数据类型
- 数字
- 字符与字符串
- s = ‘a’
- abs(s) %ASCLL码
- char(97) %字符
- num2str(65) %数字
- length(str) %计算字符串的长度
- 矩阵
- A = [1 2 3; 4 5 2; 3 2 7] %空格或逗号分开,分号换行
- B = A' %转置
- C = A(:) %按列拉伸输出
- D =inv(A) %求逆
- A * D %结果为单位矩阵E
- E = zeros(10,5,3) %三个维度的十行五列的零矩阵
- E(:,:,1) = rand(10,5) %给第一维度赋值,10行5列
- E(:,:,2) = randi(5,10,5) %最大值为5的随机整数,包括5
- E(:,:,3) = randn(10,5)
- 元胞数组
- 数组的一种,其内部元素可以是属于不同的数据类型
- A = cell(1,6) %{0×0 double} {0×0 double} {0×0 double} {0×0 double} {0×0 double} {0×0 double}
- A{2} = eye(3) %索引从1开始,{3×3 double},三阶单位阵
- magic:用来生成n阶幻方。比如三阶幻方就是1-9九个数字,组成一个3*3的矩阵,使得该矩阵无论横、竖还是斜三个方向的三个数的和总是相同。magic(n):生成一个n阶幻方,就是把1-n^2排成一个n×n的 矩阵,使得矩阵的每行、每列,以及主副对角线上面的n个数之和都相等,这个和等于n×(n^2+1)/2。
- A{5} = magic(5):五阶幻方,和为65
- 结构体
- 相当于Python中的字典
- books = struct(‘name’,{{‘Machine Learning’,‘Data Mining’}},‘price’,[30 40]) %name: {‘Machine Learning’ ‘Data Mining’} price: [30 40]
- books.name %{‘Machine Learning’} {‘Data Mining’}
- books.name(1) %{‘Machine Learning’},结果为cell
- books.name{1} %‘Machine Learning’,结果为值
清空环境变量及命令:
- clc %清空命令行的所有命令
- clear all %清除右侧工作区的所有变量
注释:
- %%注释当前行,有横线
- %没有横线
rand、randi和randn的区别?
- rand:生成均匀分布的伪随机数。分布在(0~1)之间
- rand(m,n):生成m行n列的均匀分布的伪随机数
- rand(m,n,‘double’):生成指定精度的均匀分布的伪随机数,参数还可以是’single'
- rand(RandStream,m,n):利用指定的RandStream(随机种子)生成的伪随机数
- randn:生成标准状态分布的伪随机数(均值为0,方差为1)
- 同上
- randi:生成均为分布的伪随机整数
- randi(iMax):在(0,iMax)生成均匀分布的伪随机整数
- randi(iMax,m,n):在(0,iMax]生成m×n型随机矩阵(m行n列)
- randi([iMin,iMax],m,n):在(iMin,iMax)生成m×n型随机矩阵
MATLAB矩阵操作
-
矩阵的定义与构造
- A = [1 2 3 4 5 6] %1 2 3 4 5 6
- B = 1:2:9 %1-9步长为2,13579
- C = repmat(B,3,1) %重复三行一列B
- D = ones(2,4) %两行四列均为1的矩阵
-
矩阵的四则运算
-
A=[1 2 3 4;5 6 7 8]
B=[1 1 2 2;2 2 1 1]
-
C = A+B %矩阵相加
-
D = A-B %矩阵相减
-
E = A*B' %矩阵相乘,转置
-
F = A.*B %对应项相乘
-
G = A/B %相当于A乘B的逆
-
H = A./B %对应项相除
-
-
矩阵的下标
- A =magic(5)
- B = A(2,3) %第二行第三列,下标从1开始
- C = A(3,:) %第三行
- D = A(:,4) %第四列
- [m,n] = find(A>20)%找大于20的序号值/矩阵,返回的是行和列的值
MATLAB逻辑与流程控制
-
if … else … end
1 2 3 4 5 6 7 8 9if 条件表达式 语句体 end if 表达式 语句体1 else 语句体2 end -
for … end
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15for 循环变量=初值:步长:终值 执行语句; end for n=1:5 sum=sum+n^2; end for i=1:5 p=1; for j=1:i p=p*j end sum=sum+p; end其中,步长的默认值为1,可以省略;初值、步长、终值可以是正数也可以是负数,也可以是小数
-
while … end
1 2 3while 条件表达式 执行语句 end -
switch … case … end
1 2 3 4 5 6 7 8 9switch 表达式(数值或字符串) case 数值或字符串1 语句体1; case 数值或字符串2 语句体2; ... otherwise 语句体n; end
MATLAB基本绘图操作:
1、二维平面绘图
|
|
- 颜色选项参数:r,g,b,y
- 线型选项参数:-,–,:,-.
- 数据标记点选项参数:.,+,○,*,×…
|
|
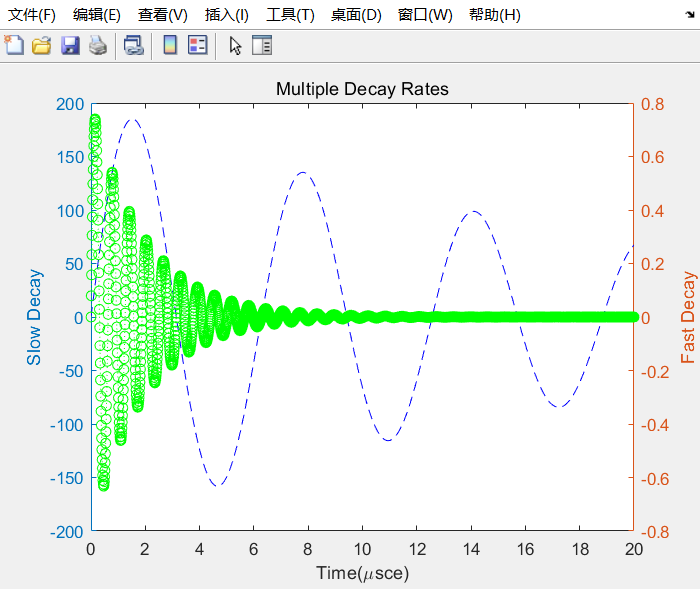
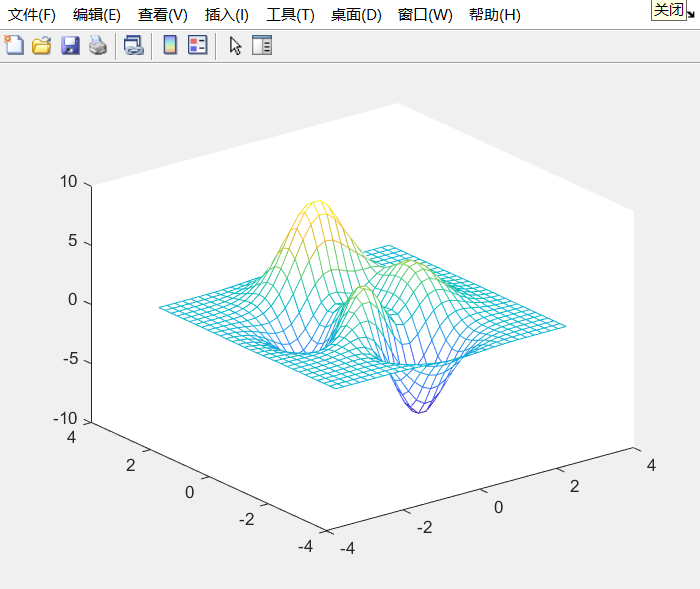
2、三维立体绘图
|
|
3、图形的保存与导出
- 编辑-复制粘贴
- 文件-另存为
- 文件-导出设置
|
|
傅里叶变换
为什么进行傅里叶变换?
- 傅里叶变换->信号的分解过程
- 时域上的原信号->分解成一系列频率下的正弦余弦信号
- 正弦信号的表示->频率频幅/频率相位->频谱图
- 傅里叶变换的好处->正弦信号的特点
- 正弦信号比原信号更简单->已被充分的研究
- 处理正弦信号->比处理原信号更简单
- 线性系统->正弦信号的频率保持性
- 输入正弦信号->输出仍是同频率的正弦信号
- 幅值和相位可能会发生变化->但频率与输入信号保持一致
- 频率保持性具有很高的工程实用价值
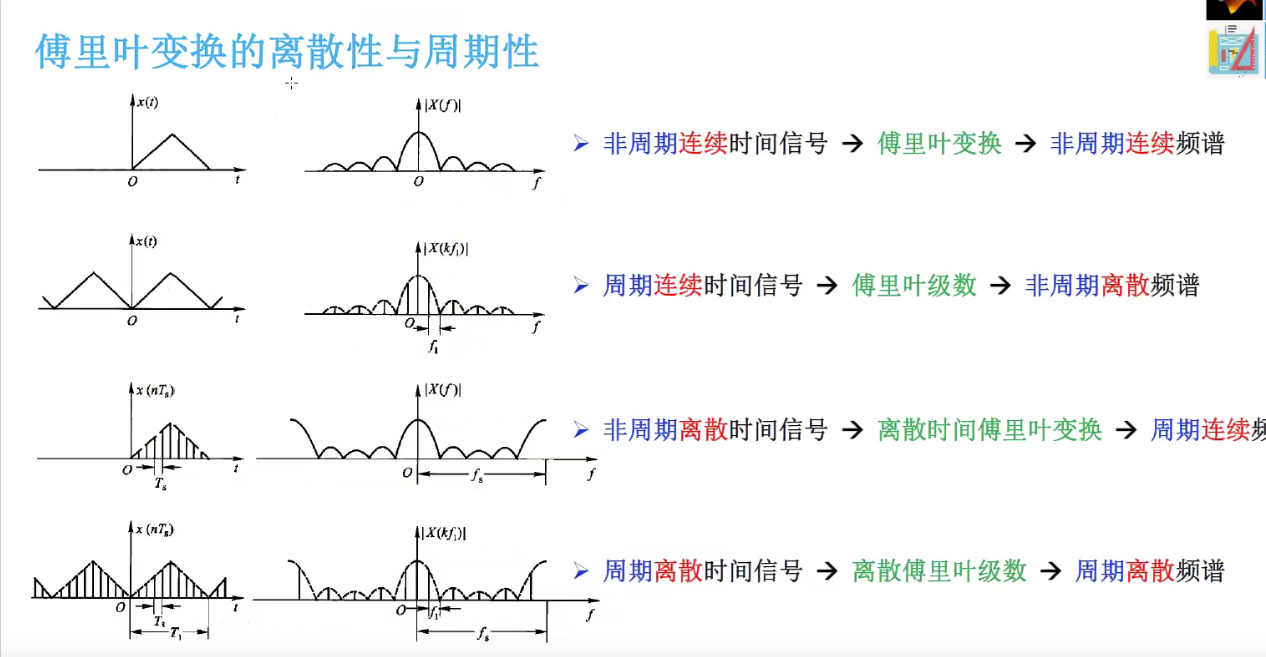
频域
在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。
傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation)
傅里叶级数(Fourier Series)的频谱
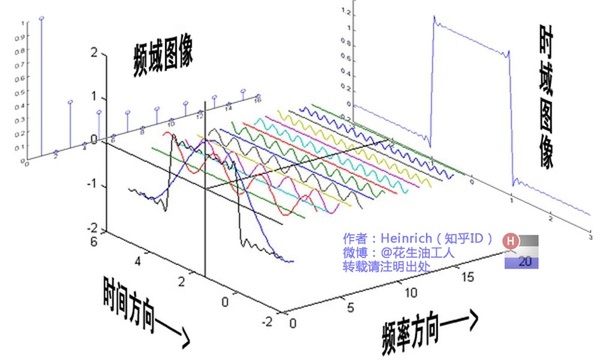

我把sin(3x)+sin(5x)的曲线给你,但是前提是你不知道这个曲线的方程式,现在需要你把sin(5x)给我从图里拿出去,看看剩下的是什么。这基本是不可能做到的。
但是在频域呢?则简单的很,无非就是几条竖线而已。
所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。
傅里叶级数(Fourier Series)的相位谱

鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢?为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。

时间差并不是相位差。如果将全部周期看作2Pi或者360度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi,就得到了相位差。
在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。所以,频谱是从侧面看,相位谱是从下面看。

傅里叶变换(Fourier Tranformation)
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波
往昔连续非周期,
回忆周期不连续,
任你ZT、DFT,
还原不回去。
往昔是一个连续的非周期信号,而回忆是一个周期离散信号。
比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。

为了方便大家对比,我们这次从另一个角度来看频谱,还是傅里叶级数中用到最多的那幅图,我们从频率较高的方向看。

以上是离散谱,那么连续谱是什么样子呢?

通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
欧拉公式
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1 的平方根,可是它真正的意义是什么呢?
 这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以 3 的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1 的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了 180 度。
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以 3 的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1 的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了 180 度。
我们知道乘-1 其实就是乘了两次 i 使线段旋转了 180 度,那么乘一次 i 呢——答案很简单——旋转了 90 度。

同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能——旋转。
 这个公式在数学领域的意义要远大于傅里叶分析,它的特殊形式——当x等于 Pi 的时候。
这个公式在数学领域的意义要远大于傅里叶分析,它的特殊形式——当x等于 Pi 的时候。

这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:

欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
关于复数更深的理解,大家可以参考:
指数形式的傅里叶变换
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。
fplot:绘制表达式或函数
fourier:傅里叶变换
ifourier:逆傅里叶变换
假设一个信号x(t)=2cos(pait)+3cos(2pait)+cos(3pait),建立这个信号被干扰的一个模型,然后计算FFT检查信号的频谱时间选10秒。
|
|
解析MATLAB短时傅里叶变换函数spectrogram()
|
|
matlab时频分析之短时傅里叶变换 spectrogram
|
|
Matlab中短时傅里叶变换 spectrogram和stft的用法
|
|
- x表示输入信号;
- window表示窗函数,如果window的值是一个整数,那么被分段的x的每一段的长度都等于window,并采用默认的Hamming窗;如果window是一个向量,那么被分段后每一段的长度都等于length(window),且输入的向量即为所要加的窗函数;
- overlap表示两段之间的重合点数,overlap的值必须要小于窗长,如果没有指定overlap,默认是窗长的一半,即50%的overlap;
- nfft表示fft的点数,fft的点数跟窗长可以是不同的,当没有指定该参数时,Matlab会取max(256, 2^(ceil(log2(length(window))))),即当窗长小于256时,fft的点数是256;当窗长大于256时,fft的点数取大于窗长的最小的2的整数次幂;
- fs表示采样率,用来归一化显示使用;
- f表示显示的频谱范围,f是一个向量,长度跟s的行数相同; 当x是实信号且nfft为偶数时,s的行数为(nfft/2+1) 当x是实信号且nfft为奇数时,s的行数为(nfft+1)/2 当x是复信号时,s的行数为nfft 当在输入的参数列表中指定f后,函数会在f指定的频率处计算频谱图,返回的f跟输入的f是相同的;
- t表示显示的时间范围,是一个向量,长度跟s的列数相同;
- p表示功率谱密度,对于实信号,p是各段PSD的单边周期估计;对于复信号,当指定F频率向量时,P为双边PSD;
Author kong
LastMod 2021-09-19